Note
Click here to download the full example code
Algorithm: RegAdaptiveProjection#
:: _label_algorithm_regadaptive_projection:
# Windows users have to encapsulate the code into a main function to avoid multiprocessing errors.
# def main():
import pygpc
import numpy as np
from collections import OrderedDict
fn_results = 'tmp/regadaptiveprojection' # filename of output
save_session_format = ".pkl" # file format of saved gpc session ".hdf5" (slow) or ".pkl" (fast)
Loading the model and defining the problem#
# define model
model = pygpc.testfunctions.GenzOscillatory()
# define problem
parameters = OrderedDict()
parameters["x1"] = pygpc.Beta(pdf_shape=[1., 1.], pdf_limits=[0., 1.])
parameters["x2"] = pygpc.Beta(pdf_shape=[1., 1.], pdf_limits=[0., 1.])
problem = pygpc.Problem(model, parameters)
Setting up the algorithm#
# gPC options
options = dict()
options["order_start"] = 2
options["order_end"] = 15
options["interaction_order"] = 2
options["solver"] = "Moore-Penrose"
options["settings"] = None
options["seed"] = 1
options["matrix_ratio"] = 2
options["n_cpu"] = 0
options["fn_results"] = fn_results
options["save_session_format"] = save_session_format
options["adaptive_sampling"] = False
options["gradient_enhanced"] = True
options["gradient_calculation"] = "FD_1st"
options["gradient_calculation_options"] = {"dx": 0.5, "distance_weight": -2}
options["n_grid_gradient"] = 5
options["qoi"] = 0
options["error_type"] = "loocv"
options["eps"] = 1e-3
options["grid"] = pygpc.Random
options["grid_options"] = {"seed": 1}
# define algorithm
algorithm = pygpc.RegAdaptiveProjection(problem=problem, options=options)
Running the gpc#
# Initialize gPC Session
session = pygpc.Session(algorithm=algorithm)
# run gPC algorithm
session, coeffs, results = session.run()
Creating initial grid (<class 'pygpc.Grid.Random'>) with n_grid=5
Performing 5 simulations!
It/Sub-it: 2/2 Performing simulation 1 from 5 [======== ] 20.0%
Total function evaluation: 0.003041982650756836 sec
It/Sub-it: 2/2 Performing simulation 01 from 10 [==== ] 10.0%
Gradient evaluation: 0.0006368160247802734 sec
Order/Interaction order: 2/2
============================
Extending grid from 5 to 6 by 1 sampling points
Performing simulations 6 to 6
It/Sub-it: 2/2 Performing simulation 1 from 1 [========================================] 100.0%
Total parallel function evaluation: 0.0032444000244140625 sec
Gradient evaluation: 0.00023293495178222656 sec
Dimension of reduced problem: 1
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 1 from 6 [====== ] 16.7%
LOOCV 2 from 6 [============= ] 33.3%
LOOCV 3 from 6 [==================== ] 50.0%
LOOCV 4 from 6 [========================== ] 66.7%
LOOCV 5 from 6 [================================= ] 83.3%
LOOCV 6 from 6 [========================================] 100.0%
LOOCV computation time: 0.0012402534484863281 sec
-> relative loocv error = 3.6811576249142592
Order/Interaction order: 3/1
============================
Extending grid from 6 to 8 by 2 sampling points
Performing simulations 7 to 8
It/Sub-it: 3/1 Performing simulation 1 from 2 [==================== ] 50.0%
Total parallel function evaluation: 0.0024416446685791016 sec
Gradient evaluation: 0.00023937225341796875 sec
Dimension of reduced problem: 1
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 1 from 8 [===== ] 12.5%
LOOCV 2 from 8 [========== ] 25.0%
LOOCV 3 from 8 [=============== ] 37.5%
LOOCV 4 from 8 [==================== ] 50.0%
LOOCV 5 from 8 [========================= ] 62.5%
LOOCV 6 from 8 [============================== ] 75.0%
LOOCV 7 from 8 [=================================== ] 87.5%
LOOCV 8 from 8 [========================================] 100.0%
LOOCV computation time: 0.0015459060668945312 sec
-> relative loocv error = 2.13194960305878
Order/Interaction order: 4/1
============================
Extending grid from 8 to 10 by 2 sampling points
Performing simulations 9 to 10
It/Sub-it: 4/1 Performing simulation 1 from 2 [==================== ] 50.0%
Total parallel function evaluation: 0.002061605453491211 sec
Gradient evaluation: 0.00024437904357910156 sec
Dimension of reduced problem: 1
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 10 [==== ] 10.0%
LOOCV 02 from 10 [======== ] 20.0%
LOOCV 03 from 10 [============ ] 30.0%
LOOCV 04 from 10 [================ ] 40.0%
LOOCV 05 from 10 [==================== ] 50.0%
LOOCV 06 from 10 [======================== ] 60.0%
LOOCV 07 from 10 [============================ ] 70.0%
LOOCV 08 from 10 [================================ ] 80.0%
LOOCV 09 from 10 [==================================== ] 90.0%
LOOCV 10 from 10 [========================================] 100.0%
LOOCV computation time: 0.0020117759704589844 sec
-> relative loocv error = 1.358930829487926
Order/Interaction order: 5/1
============================
Extending grid from 10 to 12 by 2 sampling points
Performing simulations 11 to 12
It/Sub-it: 5/1 Performing simulation 1 from 2 [==================== ] 50.0%
Total parallel function evaluation: 0.0022783279418945312 sec
Gradient evaluation: 0.00028586387634277344 sec
Dimension of reduced problem: 1
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 12 [=== ] 8.3%
LOOCV 02 from 12 [====== ] 16.7%
LOOCV 03 from 12 [========== ] 25.0%
LOOCV 04 from 12 [============= ] 33.3%
LOOCV 05 from 12 [================ ] 41.7%
LOOCV 06 from 12 [==================== ] 50.0%
LOOCV 07 from 12 [======================= ] 58.3%
LOOCV 08 from 12 [========================== ] 66.7%
LOOCV 09 from 12 [============================== ] 75.0%
LOOCV 10 from 12 [================================= ] 83.3%
LOOCV 11 from 12 [==================================== ] 91.7%
LOOCV 12 from 12 [========================================] 100.0%
LOOCV computation time: 0.0024056434631347656 sec
-> relative loocv error = 0.07107706753980376
Order/Interaction order: 6/1
============================
Extending grid from 12 to 14 by 2 sampling points
Performing simulations 13 to 14
It/Sub-it: 6/1 Performing simulation 1 from 2 [==================== ] 50.0%
Total parallel function evaluation: 0.002135038375854492 sec
Gradient evaluation: 0.0006742477416992188 sec
Dimension of reduced problem: 1
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 14 [== ] 7.1%
LOOCV 02 from 14 [===== ] 14.3%
LOOCV 03 from 14 [======== ] 21.4%
LOOCV 04 from 14 [=========== ] 28.6%
LOOCV 05 from 14 [============== ] 35.7%
LOOCV 06 from 14 [================= ] 42.9%
LOOCV 07 from 14 [==================== ] 50.0%
LOOCV 08 from 14 [====================== ] 57.1%
LOOCV 09 from 14 [========================= ] 64.3%
LOOCV 10 from 14 [============================ ] 71.4%
LOOCV 11 from 14 [=============================== ] 78.6%
LOOCV 12 from 14 [================================== ] 85.7%
LOOCV 13 from 14 [===================================== ] 92.9%
LOOCV 14 from 14 [========================================] 100.0%
LOOCV computation time: 0.002898693084716797 sec
-> relative loocv error = 0.24330465952490127
Order/Interaction order: 7/1
============================
Extending grid from 14 to 16 by 2 sampling points
Performing simulations 15 to 16
It/Sub-it: 7/1 Performing simulation 1 from 2 [==================== ] 50.0%
Total parallel function evaluation: 0.0045604705810546875 sec
Gradient evaluation: 0.0020012855529785156 sec
Dimension of reduced problem: 2
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 16 [== ] 6.2%
LOOCV 02 from 16 [===== ] 12.5%
LOOCV 03 from 16 [======= ] 18.8%
LOOCV 04 from 16 [========== ] 25.0%
LOOCV 05 from 16 [============ ] 31.2%
LOOCV 06 from 16 [=============== ] 37.5%
LOOCV 07 from 16 [================= ] 43.8%
LOOCV 08 from 16 [==================== ] 50.0%
LOOCV 09 from 16 [====================== ] 56.2%
LOOCV 10 from 16 [========================= ] 62.5%
LOOCV 11 from 16 [=========================== ] 68.8%
LOOCV 12 from 16 [============================== ] 75.0%
LOOCV 13 from 16 [================================ ] 81.2%
LOOCV 14 from 16 [=================================== ] 87.5%
LOOCV 15 from 16 [===================================== ] 93.8%
LOOCV 16 from 16 [========================================] 100.0%
LOOCV computation time: 0.004574775695800781 sec
-> relative loocv error = 0.41878269925997813
Order/Interaction order: 7/2
============================
Extending grid from 16 to 72 by 56 sampling points
Performing simulations 17 to 72
It/Sub-it: 7/2 Performing simulation 01 from 56 [ ] 1.8%
Total parallel function evaluation: 0.002550363540649414 sec
Gradient evaluation: 0.007954597473144531 sec
Dimension of reduced problem: 2
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 25 [= ] 4.0%
LOOCV 02 from 25 [=== ] 8.0%
LOOCV 03 from 25 [==== ] 12.0%
LOOCV 04 from 25 [====== ] 16.0%
LOOCV 05 from 25 [======== ] 20.0%
LOOCV 06 from 25 [========= ] 24.0%
LOOCV 07 from 25 [=========== ] 28.0%
LOOCV 08 from 25 [============ ] 32.0%
LOOCV 09 from 25 [============== ] 36.0%
LOOCV 10 from 25 [================ ] 40.0%
LOOCV 11 from 25 [================= ] 44.0%
LOOCV 12 from 25 [=================== ] 48.0%
LOOCV 13 from 25 [==================== ] 52.0%
LOOCV 14 from 25 [====================== ] 56.0%
LOOCV 15 from 25 [======================== ] 60.0%
LOOCV 16 from 25 [========================= ] 64.0%
LOOCV 17 from 25 [=========================== ] 68.0%
LOOCV 18 from 25 [============================ ] 72.0%
LOOCV 19 from 25 [============================== ] 76.0%
LOOCV 20 from 25 [================================ ] 80.0%
LOOCV 21 from 25 [================================= ] 84.0%
LOOCV 22 from 25 [=================================== ] 88.0%
LOOCV 23 from 25 [==================================== ] 92.0%
LOOCV 24 from 25 [====================================== ] 96.0%
LOOCV 25 from 25 [========================================] 100.0%
LOOCV computation time: 0.03264451026916504 sec
-> relative loocv error = 0.14322261868055872
Order/Interaction order: 8/1
============================
Extending grid from 72 to 76 by 4 sampling points
Performing simulations 73 to 76
It/Sub-it: 8/1 Performing simulation 1 from 4 [========== ] 25.0%
Total parallel function evaluation: 0.004721641540527344 sec
Gradient evaluation: 0.021195411682128906 sec
Dimension of reduced problem: 2
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 25 [= ] 4.0%
LOOCV 02 from 25 [=== ] 8.0%
LOOCV 03 from 25 [==== ] 12.0%
LOOCV 04 from 25 [====== ] 16.0%
LOOCV 05 from 25 [======== ] 20.0%
LOOCV 06 from 25 [========= ] 24.0%
LOOCV 07 from 25 [=========== ] 28.0%
LOOCV 08 from 25 [============ ] 32.0%
LOOCV 09 from 25 [============== ] 36.0%
LOOCV 10 from 25 [================ ] 40.0%
LOOCV 11 from 25 [================= ] 44.0%
LOOCV 12 from 25 [=================== ] 48.0%
LOOCV 13 from 25 [==================== ] 52.0%
LOOCV 14 from 25 [====================== ] 56.0%
LOOCV 15 from 25 [======================== ] 60.0%
LOOCV 16 from 25 [========================= ] 64.0%
LOOCV 17 from 25 [=========================== ] 68.0%
LOOCV 18 from 25 [============================ ] 72.0%
LOOCV 19 from 25 [============================== ] 76.0%
LOOCV 20 from 25 [================================ ] 80.0%
LOOCV 21 from 25 [================================= ] 84.0%
LOOCV 22 from 25 [=================================== ] 88.0%
LOOCV 23 from 25 [==================================== ] 92.0%
LOOCV 24 from 25 [====================================== ] 96.0%
LOOCV 25 from 25 [========================================] 100.0%
LOOCV computation time: 0.03430962562561035 sec
-> relative loocv error = 0.0527976297089744
Order/Interaction order: 8/2
============================
Extending grid from 76 to 90 by 14 sampling points
Performing simulations 77 to 90
It/Sub-it: 8/2 Performing simulation 01 from 14 [== ] 7.1%
Total parallel function evaluation: 0.004903078079223633 sec
Gradient evaluation: 0.023989200592041016 sec
Dimension of reduced problem: 2
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 25 [= ] 4.0%
LOOCV 02 from 25 [=== ] 8.0%
LOOCV 03 from 25 [==== ] 12.0%
LOOCV 04 from 25 [====== ] 16.0%
LOOCV 05 from 25 [======== ] 20.0%
LOOCV 06 from 25 [========= ] 24.0%
LOOCV 07 from 25 [=========== ] 28.0%
LOOCV 08 from 25 [============ ] 32.0%
LOOCV 09 from 25 [============== ] 36.0%
LOOCV 10 from 25 [================ ] 40.0%
LOOCV 11 from 25 [================= ] 44.0%
LOOCV 12 from 25 [=================== ] 48.0%
LOOCV 13 from 25 [==================== ] 52.0%
LOOCV 14 from 25 [====================== ] 56.0%
LOOCV 15 from 25 [======================== ] 60.0%
LOOCV 16 from 25 [========================= ] 64.0%
LOOCV 17 from 25 [=========================== ] 68.0%
LOOCV 18 from 25 [============================ ] 72.0%
LOOCV 19 from 25 [============================== ] 76.0%
LOOCV 20 from 25 [================================ ] 80.0%
LOOCV 21 from 25 [================================= ] 84.0%
LOOCV 22 from 25 [=================================== ] 88.0%
LOOCV 23 from 25 [==================================== ] 92.0%
LOOCV 24 from 25 [====================================== ] 96.0%
LOOCV 25 from 25 [========================================] 100.0%
LOOCV computation time: 0.05082130432128906 sec
-> relative loocv error = 0.041595165319890964
Order/Interaction order: 9/1
============================
Extending grid from 90 to 94 by 4 sampling points
Performing simulations 91 to 94
It/Sub-it: 9/1 Performing simulation 1 from 4 [========== ] 25.0%
Total parallel function evaluation: 0.004591703414916992 sec
Gradient evaluation: 0.02653956413269043 sec
Dimension of reduced problem: 2
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
LOOCV 01 from 25 [= ] 4.0%
LOOCV 02 from 25 [=== ] 8.0%
LOOCV 03 from 25 [==== ] 12.0%
LOOCV 04 from 25 [====== ] 16.0%
LOOCV 05 from 25 [======== ] 20.0%
LOOCV 06 from 25 [========= ] 24.0%
LOOCV 07 from 25 [=========== ] 28.0%
LOOCV 08 from 25 [============ ] 32.0%
LOOCV 09 from 25 [============== ] 36.0%
LOOCV 10 from 25 [================ ] 40.0%
LOOCV 11 from 25 [================= ] 44.0%
LOOCV 12 from 25 [=================== ] 48.0%
LOOCV 13 from 25 [==================== ] 52.0%
LOOCV 14 from 25 [====================== ] 56.0%
LOOCV 15 from 25 [======================== ] 60.0%
LOOCV 16 from 25 [========================= ] 64.0%
LOOCV 17 from 25 [=========================== ] 68.0%
LOOCV 18 from 25 [============================ ] 72.0%
LOOCV 19 from 25 [============================== ] 76.0%
LOOCV 20 from 25 [================================ ] 80.0%
LOOCV 21 from 25 [================================= ] 84.0%
LOOCV 22 from 25 [=================================== ] 88.0%
LOOCV 23 from 25 [==================================== ] 92.0%
LOOCV 24 from 25 [====================================== ] 96.0%
LOOCV 25 from 25 [========================================] 100.0%
LOOCV computation time: 0.0492861270904541 sec
-> relative loocv error = 0.0009811310203238616
Determine gPC coefficients using 'Moore-Penrose' solver (gradient enhanced)...
Postprocessing#
# read session
session = pygpc.read_session(fname=session.fn_session, folder=session.fn_session_folder)
# Post-process gPC
pygpc.get_sensitivities_hdf5(fn_gpc=options["fn_results"],
output_idx=None,
calc_sobol=True,
calc_global_sens=True,
calc_pdf=True,
algorithm="sampling",
n_samples=1e3)
> Loading gpc session object: tmp/regadaptiveprojection.pkl
> Loading gpc coeffs: tmp/regadaptiveprojection.hdf5
> Adding results to: tmp/regadaptiveprojection.hdf5
Validation#
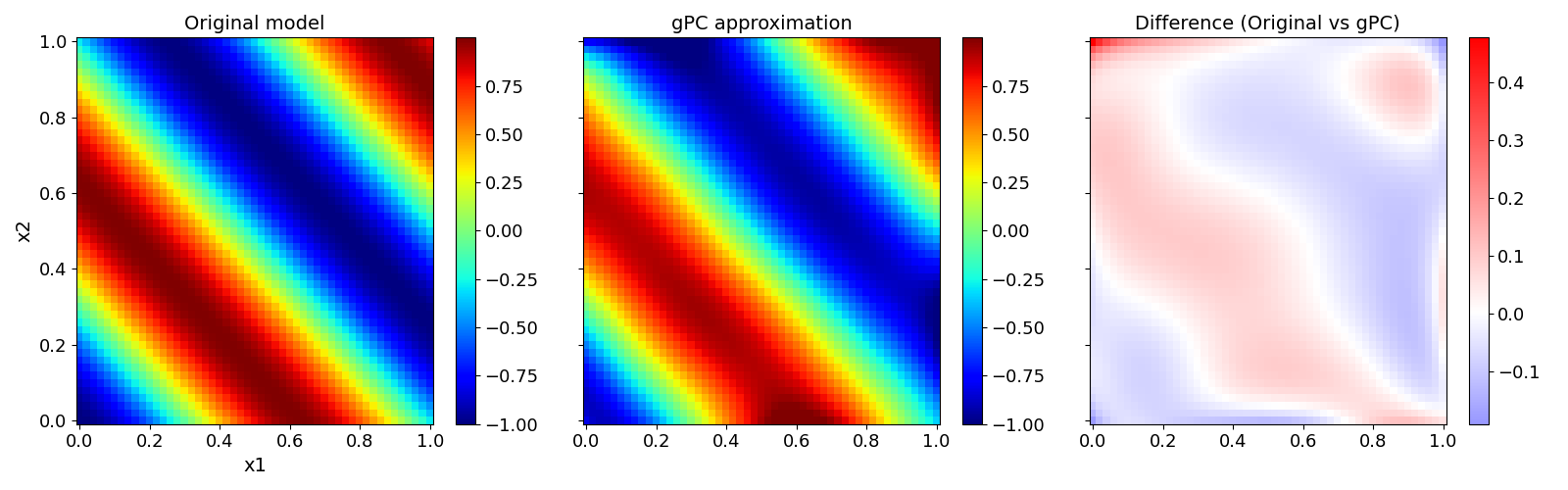
Validate gPC vs original model function (2D-surface)#
pygpc.validate_gpc_plot(session=session,
coeffs=coeffs,
random_vars=list(problem.parameters_random.keys()),
n_grid=[51, 51],
output_idx=[0],
fn_out=None,
folder=None,
n_cpu=session.n_cpu)
Validate gPC vs original model function (Monte Carlo)#
nrmsd = pygpc.validate_gpc_mc(session=session,
coeffs=coeffs,
n_samples=int(1e4),
output_idx=[0],
fn_out=None,
folder=None,
plot=True,
n_cpu=session.n_cpu)
print("> Maximum NRMSD (gpc vs original): {:.2}%".format(max(nrmsd)))
# On Windows subprocesses will import (i.e. execute) the main module at start.
# You need to insert an if __name__ == '__main__': guard in the main module to avoid
# creating subprocesses recursively.
#
# if __name__ == '__main__':
# main()
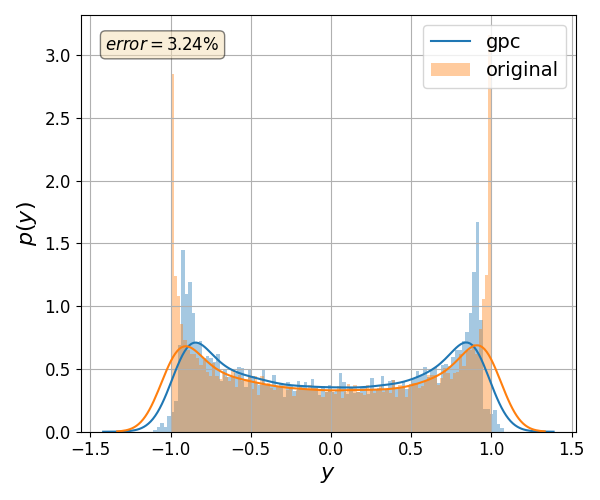
> Maximum NRMSD (gpc vs original): 0.032%
Total running time of the script: ( 0 minutes 2.806 seconds)